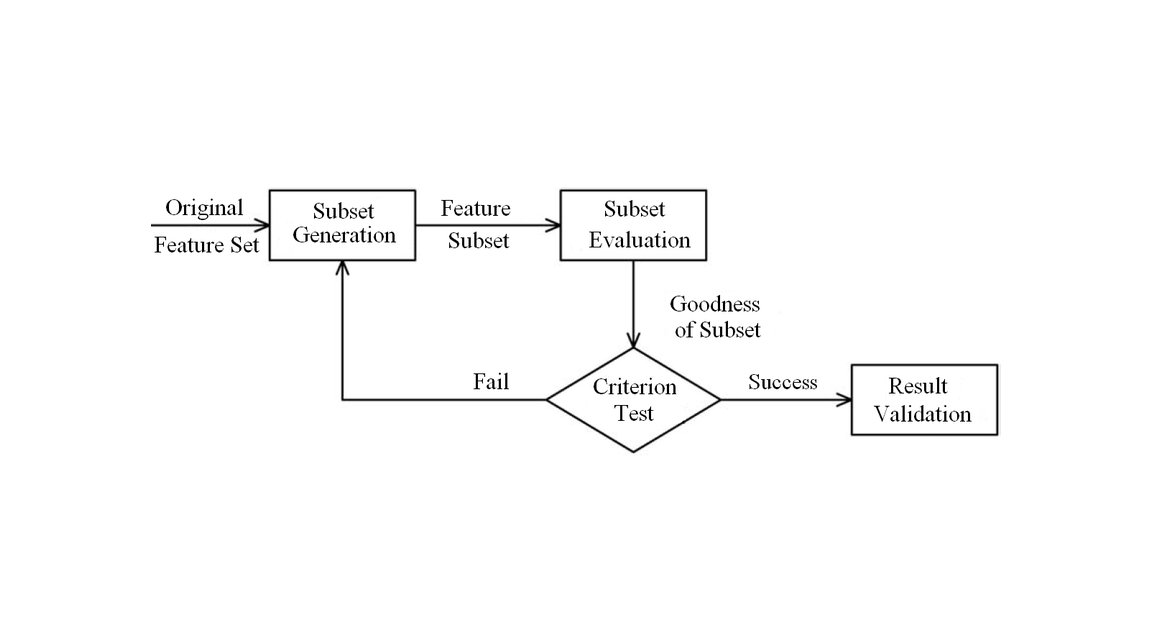
Feature selection in machine learning

The concept of “garbage in–garbage out” applies when building a data-driven predictive model.  The time for training a model increase exponentially with the number of features. Too many features also becomes a hurdle when attempting to select meaningful features. Moreover, the risk of overfitting increases as the number of features increases given limited number of data points. Thus, selecting or extracting informative features is a critical step when building a data-driven model. Feature selection refers to a process in which a subset of features of the whole feature set is selected whereas feature extraction usually involves transforming a feature or merging multiple features with new features generated.

In developing a data-driven model, feature selection can be implemented separately from training a model or embedded in the process of model-training. As a separate step, feature selection can be implemented by a filter approach or a wrapper approach. For a filter approach, a criterion defining the correlation or mutual information between a feature and the dependent variable serves as the filter to screen features. A wrapper approach measures the usefulness of a feature in terms of its contribution to improving the model’s performance in cross-validation. The term wrapper approach serves as an umbrella term under which sequential feature selection (SFS) algorithm and genetic algorithms are encapsulated. Sequential forward selection is a special case of SFS, which starts with an empty subset and selects the feature which brings the highest improvement among all the left features until adding more features does not help improve prediction performance. In general, wrapper approaches takes far more computation time than filter approaches as we have to train the model and conduct cross validation for each selected subset. An embedded feature selection approach is achieved based on the weights of the features generated when training the model is finished. Usually a penalty is applied to the norm of the weights, which restrict the weights of some features to be small (e.g. L2 penalty used in Ridge regression) or exactly zero (e.g. L1 penalty in Lasso regression). For a specific category of model, the importance of a feature can be computed based on the trained model e.g. feature importance in tree based models are calculated based on Gini Index, Entropy or Chi-Square value.

References:

Cai, Jie, et al. “Feature selection in machine learning: A new perspective.” Neurocomputing 300 (2018): 70-79.